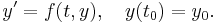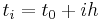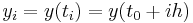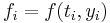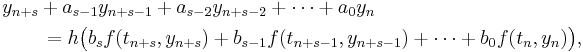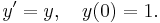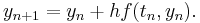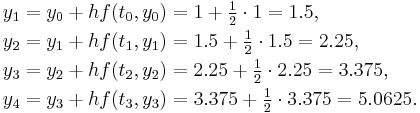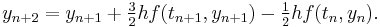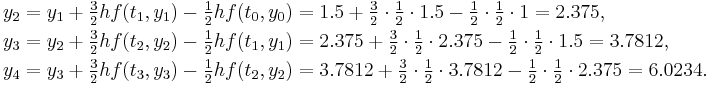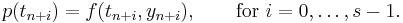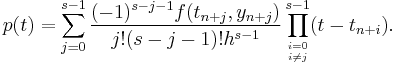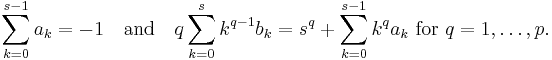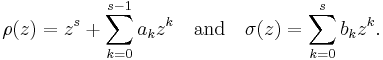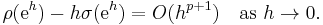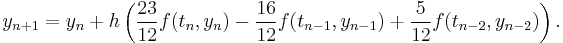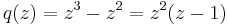Linear multistep method
Linear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the solution. Single-step methods (such as Euler's method) refer to only one previous point and its derivative to determine the current value. Methods such as Runge-Kutta take some intermediate steps (for example, a half-step) to obtain a higher order method, but then discard all previous information before taking a second step. Multistep methods attempt to gain efficiency by keeping and using the information from previous steps rather than discarding it. Consequently, multistep methods refer to several previous points and derivative values. In the case of linear multistep methods, a linear combination of the previous points and derivative values is used.
Contents |
Definitions
Numerical methods for ordinary differential equations approximate solutions to initial value problems of the form
The result is approximations for the value of 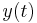 at discrete times
at discrete times 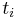 :
:
where h is the time step (sometimes referred to as 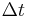 ).
).
A linear multistep method uses a linear combination of 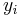 and
and 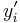 to calculate the value of y for the desired current step.
to calculate the value of y for the desired current step.
Multistep method will use the previous s steps to calculate the next value. Consequently, the desired value at the current processing stage is 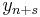 .
.
A linear multistep method is a method of the form
where h denotes the step size and f the right-hand side of the differential equation. The coefficients 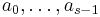 and
and  determine the method. The designer of the method chooses the coefficients; often, many coefficients are zero. Typically, the designer chooses the coefficients so they will exactly interpolate
determine the method. The designer of the method chooses the coefficients; often, many coefficients are zero. Typically, the designer chooses the coefficients so they will exactly interpolate 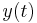 when it is an nth order polynomial.
when it is an nth order polynomial.
If 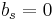 , then the method is called "explicit", since the formula can directly compute
, then the method is called "explicit", since the formula can directly compute 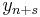 .
.
If 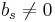 then the method is called "implicit", since the value of
then the method is called "implicit", since the value of 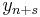 depends on the value of
depends on the value of 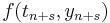 , and the equation must be solved for
, and the equation must be solved for 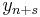 . Iterative methods such as Newton's method are often used to solve the implicit formula.
. Iterative methods such as Newton's method are often used to solve the implicit formula.
Sometimes an explicit multistep method is used to "predict" the value of 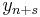 . That value is then used in an implicit formula to "correct" the value. The result is a Predictor-corrector method.
. That value is then used in an implicit formula to "correct" the value. The result is a Predictor-corrector method.
Examples
Consider for an example the problem
The exact solution is 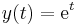 .
.
One-Step Euler
A simple numerical method is Euler's method:
Euler's method can be viewed as an explicit multistep method for the degenerate case of one step.
This method, applied with step size 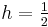 on the problem
on the problem 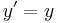 , gives the following results:
, gives the following results:
Two-Step Adams Bashforth
Euler's method is a one-step method. A simple multistep method is the two-step Adams–Bashforth method
This method needs two values, 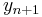 and
and 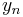 , to compute the next value,
, to compute the next value, 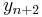 . However, the initial value problem provides only one value,
. However, the initial value problem provides only one value, 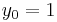 . One possibility to resolve this issue is to use the
. One possibility to resolve this issue is to use the 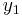 computed by Euler's method as the second value. With this choice, the Adams–Bashforth method yields (rounded to four digits):
computed by Euler's method as the second value. With this choice, the Adams–Bashforth method yields (rounded to four digits):
The exact solution at 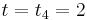 is
is 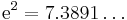 , so the two-step Adams–Bashforth method is more accurate than Euler's method. This is always the case if the step size is small enough.
, so the two-step Adams–Bashforth method is more accurate than Euler's method. This is always the case if the step size is small enough.
Multistep Method Families
Three families of linear multistep methods are commonly used: Adams–Bashforth methods, Adams–Moulton methods, and the backward differentiation formulas (BDFs).
Adams–Bashforth methods
The Adams–Bashforth methods are explicit methods. The coefficients are 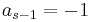 and
and 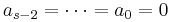 , while the
, while the 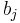 are chosen such that the methods has order s (this determines the methods uniquely).
are chosen such that the methods has order s (this determines the methods uniquely).
The Adams–Bashforth methods with s = 1, 2, 3, 4, 5 are (Hairer, Nørsett & Wanner 1993, §III.1; Butcher 2003, p. 103):
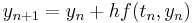 —this is simply the Euler method;
—this is simply the Euler method;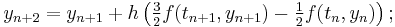
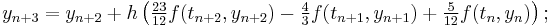
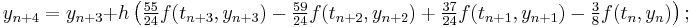
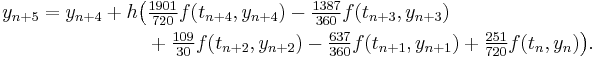
The coefficients 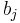 can be determined as follows. Use polynomial interpolation to find the polynomial p of degree
can be determined as follows. Use polynomial interpolation to find the polynomial p of degree  such that
such that
The Lagrange formula for polynomial interpolation yields
The polynomial p is locally a good approximation of the right-hand side of the differential equation 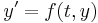 that is to be solved, so consider the equation
that is to be solved, so consider the equation 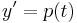 instead. This equation can be solved exactly; the solution is simply the integral of p. This suggests taking
instead. This equation can be solved exactly; the solution is simply the integral of p. This suggests taking
The Adams–Bashforth method arises when the formula for p is substituted. The coefficients 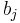 turn out to be given by
turn out to be given by
Replacing f(t, y) by its interpolant p incurs an error of order hs, and it follows that the s-step Adams–Bashforth method has indeed order s (Iserles 1996, §2.1)
The Adams–Bashforth methods were designed by John Couch Adams to solve a differential equation modelling capillary action due to Francis Bashforth. Bashforth (1883) published his theory and Adams' numerical method (Goldstine 1977).
Adams–Moulton methods
The Adams–Moulton methods are similar to the Adams–Bashforth methods in that they also have 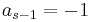 and
and 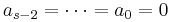 . Again the b coefficients are chosen to obtain the highest order possible. However, the Adams–Moulton methods are implicit methods. By removing the restriction that
. Again the b coefficients are chosen to obtain the highest order possible. However, the Adams–Moulton methods are implicit methods. By removing the restriction that 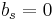 , an s-step Adams–Moulton method can reach order
, an s-step Adams–Moulton method can reach order 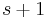 , while an s-step Adams–Bashforth methods has only order s.
, while an s-step Adams–Bashforth methods has only order s.
The Adams–Moulton methods with s = 0, 1, 2, 3, 4 are (Hairer, Nørsett & Wanner 1993, §III.1; Quarteroni, Sacco & Saleri 2000):
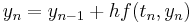 — this is the backward Euler method;
— this is the backward Euler method;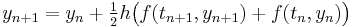 — this is the trapezoidal rule;
— this is the trapezoidal rule;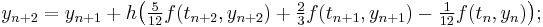
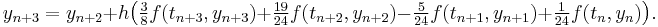
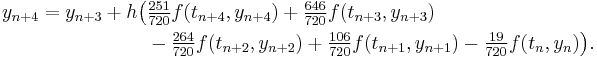
The derivation of the Adams–Moulton methods is similar to that of the Adams–Bashforth method; however, the interpolating polynomial uses not only the points tn−1, … tn−s, as above, but also 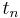 . The coefficients are given by
. The coefficients are given by
The Adams–Moulton methods are solely due to John Couch Adams, like the Adams–Bashforth methods. The name of Forest Ray Moulton became associated with these methods because he realized that they could be used in tandem with the Adams–Bashforth methods as a predictor-corrector pair (Moulton 1926); Milne (1926) had the same idea. Adams used Newton's method to solve the implicit equation (Hairer, Nørsett & Wanner 1993, §III.1).
Analysis
The central concepts in the analysis of linear multistep methods, and indeed any numerical method for differential equations, are convergence, order, and stability.
The first question is whether the method is consistent: is the difference equation
a good approximation of the differential equation 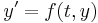 ? More precisely, a multistep method is consistent if the local error goes to zero as the step size h goes to zero, where the local error is defined to be the difference between the result
? More precisely, a multistep method is consistent if the local error goes to zero as the step size h goes to zero, where the local error is defined to be the difference between the result 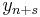 of the method, assuming that all the previous values
of the method, assuming that all the previous values 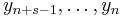 are exact, and the exact solution of the equation at time
are exact, and the exact solution of the equation at time 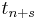 , divided by h. A computation using Taylor series shows out that a linear multistep method is consistent if and only if
, divided by h. A computation using Taylor series shows out that a linear multistep method is consistent if and only if
All the methods mentioned above are consistent (Hairer, Nørsett & Wanner 1993, §III.2).
If the method is consistent, then the next question is how well the difference equation defining the numerical method approximates the differential equation. A multistep method is said to have order p if the local error is of order 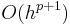 as h goes to zero. This is equivalent to the following condition on the coefficients of the methods:
as h goes to zero. This is equivalent to the following condition on the coefficients of the methods:
The s-step Adams–Bashforth method has order s, while the s-step Adams–Moulton method has order 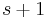 (Hairer, Nørsett & Wanner 1993, §III.2).
(Hairer, Nørsett & Wanner 1993, §III.2).
These conditions are often formulated using the characteristic polynomials
In terms of these polynomials, the above condition for the method to have order p becomes
In particular, the method is consistent if it has order one, which is the case if 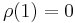 and
and  .
.
If the roots of the characteristic polynomial  all have modulus less than or equal to 1 and the roots of modulus 1 are of multiplicity 1, we say that the root condition is satisfied. The method is convergent if and only if it is consistent and the root condition is satisfied. Consequently, a consistent method is stable if and only if this condition is satisfied, and thus the method is convergent if and only if it is stable.
all have modulus less than or equal to 1 and the roots of modulus 1 are of multiplicity 1, we say that the root condition is satisfied. The method is convergent if and only if it is consistent and the root condition is satisfied. Consequently, a consistent method is stable if and only if this condition is satisfied, and thus the method is convergent if and only if it is stable.
Furthermore, if the method is stable, the method is said to be strongly stable if 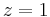 is the only root of modulus 1. If it is stable and all roots of modulus 1 are not repeated, but there is more than one such root, it is said to be relatively stable. Note that 1 must be a root; thus stable methods are always one of these two.
is the only root of modulus 1. If it is stable and all roots of modulus 1 are not repeated, but there is more than one such root, it is said to be relatively stable. Note that 1 must be a root; thus stable methods are always one of these two.
Example
Consider the Adams–Bashforth three-step method
The characteristic equation is thus
which has roots 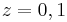 , and the conditions above are satisfied. As
, and the conditions above are satisfied. As 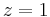 is the only root of modulus 1, the method is strongly stable.
is the only root of modulus 1, the method is strongly stable.
First and second Dahlquist barriers
These two results were proved by Germund Dahlquist and represent an important bound for the order of convergence and for the A-stability of a linear multistep method.
First Dahlquist barrier
A zero-stable and linear q-step multistep method cannot attain an order of convergence greater than q + 1 if q is odd and greater than q + 2 if q is even. If the method is also explicit, then it cannot attain an order greater than q (Hairer, Nørsett & Wanner 1993, Thm III.3.5).
Second Dahlquist barrier
There are no explicit A-stable and linear multistep methods. The implicit ones have order of convergence at most 2 (Hairer & Wanner 1996, Thm V.1.4).
See also
References
- Bashforth, Francis (1883), An Attempt to test the Theories of Capillary Action by comparing the theoretical and measured forms of drops of fluid. With an explanation of the method of integration employed in constructing the tables which give the theoretical forms of such drops, by J. C. Adams, Cambridge.
- Butcher, John C. (2003), Numerical Methods for Ordinary Differential Equations, John Wiley, ISBN 978-0-471-96758-3.
- Goldstine, Herman H. (1977), A History of Numerical Analysis from the 16th through the 19th Century, New York: Springer-Verlag, ISBN 978-0-387-90277-7.
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems (2nd ed.), Berlin: Springer Verlag, ISBN 978-3-540-56670-0.
- Hairer, Ernst; Wanner, Gerhard (1996), Solving ordinary differential equations II: Stiff and differential-algebraic problems (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-60452-5.
- Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2.
- Milne, W. E. (1926), "Numerical integration of ordinary differential equations", American Mathematical Monthly (Mathematical Association of America) 33 (9): 455–460, doi:10.2307/2299609, JSTOR 2299609.
- Moulton, Forest R. (1926), New methods in exterior ballistics, University of Chicago Press.
- Quarteroni, Alfio; Sacco, Riccardo; Saleri, Fausto (2000), Matematica Numerica, Springer Verlag, ISBN 978-8-847-00077-3
External links
- Weisstein, Eric W., "Adams Method" from MathWorld.
- Adams-Bashforth-Moulton Method
- DotNumerics: Ordinary Differential Equations for C# and VB.NET Initial-value problem for nonstiff and stiff ordinary differential equations (explicit Runge-Kutta, implicit Runge-Kutta, Gear’s BDF and Adams-Moulton).
|
|||||||||||